Светлая тема /
тёмная тема
Квартет Энскомба
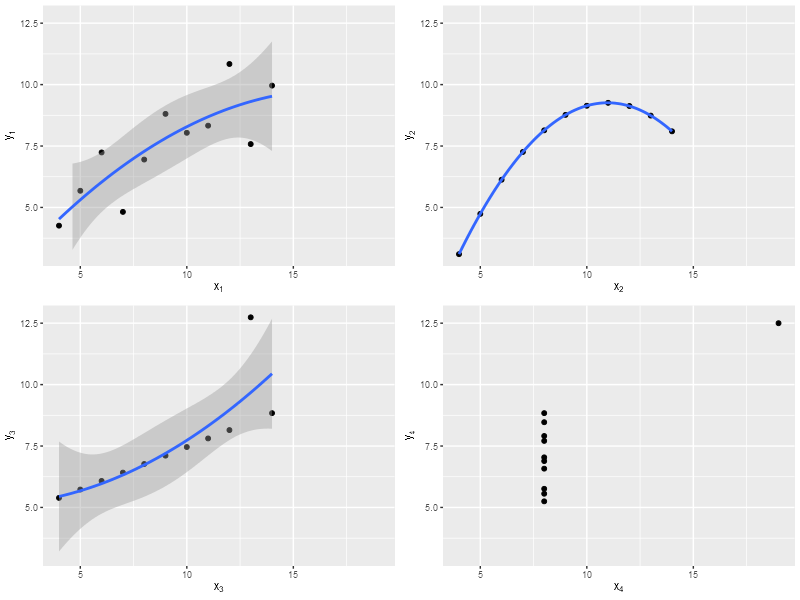
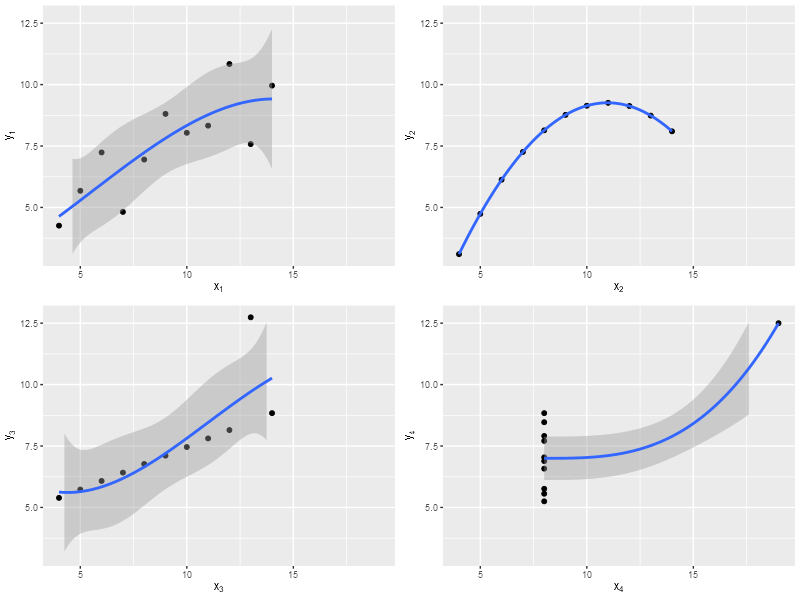
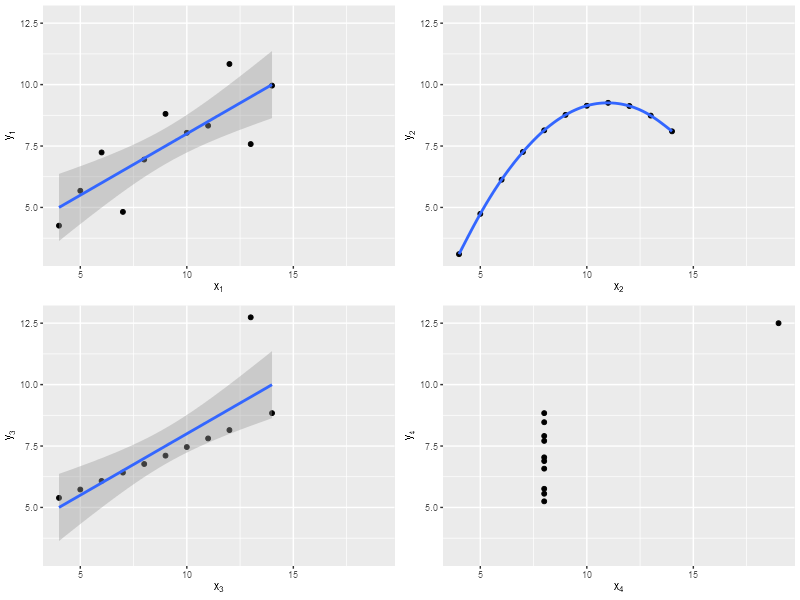
Квартет Энскомба (это английский математик) — четыре набора точек на плоскости. Их особенность в том, что каждый из четырёх наборов сильно отличается от других графически, но некоторые простые статистики совпадают.
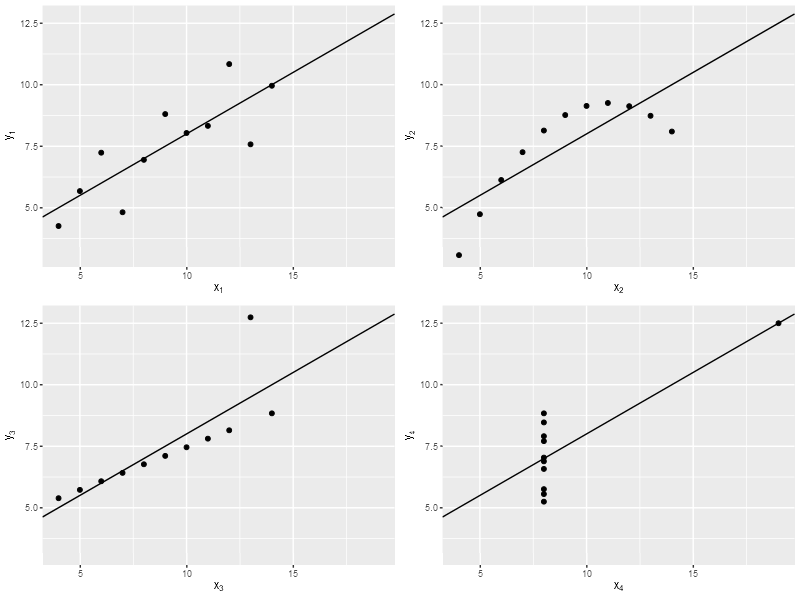
Вот эти наборы.
\(x_{1}\)
\(y_{1}\)
\(x_{2}\)
\(y_{2}\)
\(x_{3}\)
\(y_{3}\)
\(x_{4}\)
\(y_{4}\)
10,0
8,04
10,0
9,14
10,0
7,46
8,0
6,58
8,0
6,95
8,0
8,14
8,0
6,77
8,0
5,76
13,0
7,58
13,0
8,74
13,0
12,74
8,0
7,71
9,0
8,81
9,0
8,77
9,0
7,11
8,0
8,84
11,0
8,33
11,0
9,26
11,0
7,81
8,0
8,47
14,0
9,96
14,0
8,10
14,0
8,84
8,0
7,04
6,0
7,24
6,0
6,13
6,0
6,08
8,0
5,25
4,0
4,26
4,0
3,10
4,0
5,39
19,0
12,50
12,0
10,84
12,0
9,13
12,0
8,15
8,0
5,56
7,0
4,82
7,0
7,26
7,0
6,42
8,0
7,91
5,0
5,68
5,0
4,74
5,0
5,73
8,0
6,89
Статистики.
1
2
3
4
Среднее значение \(x\)
9,0
9,0
9,0
9,0
Дисперсия \(x\)
10,0
10,0
10,0
10,0
Среднее значение \(y\)
7,5
7,5
7,5
7,5
Дисперсия \(y\)
3,75
3,75
3,75
3,75
Корреляция между \(x\) и \(y\)
0,816
0,816
0,816
0,816
Результат линейной регрессии одинаковый.
Набор
Линейная регрессия
Коэффициент детерминации
линейной регрессии
линейной регрессии
1
\(y=0{,}5x+3\)
0,67
2
\(y=0{,}5x+3\)
0,67
3
\(y=0{,}5x+3\)
0,67
4
\(y=0{,}5x+3\)
0,67
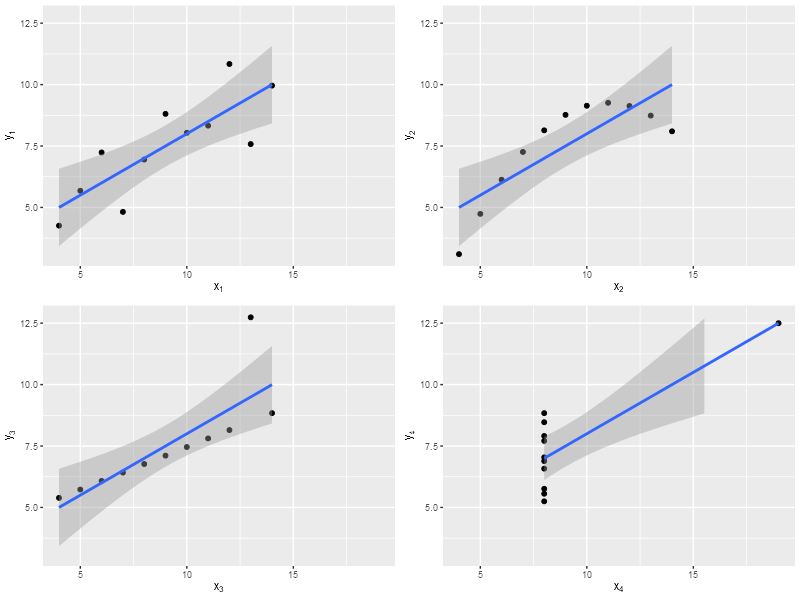
Квадратичная регрессия даёт другие результаты.
Набор
Квадратичная регрессия
1
\(y=-0{,}032x^{2}+1{,}069x+0{,}755\)
2
\(y=-0{,}127x^{2}+2{,}781x-5{,}996\)
3
\(y=0{,}03x^{2}-0{,}035x+5{,}112\)
4
\(y=1{,}945x^{2}-52{,}024x+298{,}785\)