Многорукие бандиты — это альтернатива A/B-тестированию, то есть методу обоснованного выбора между рядом вариантов. С одной стороны, это простая вещь, с другой — она имеет много применений.

Изображение: adamlane85

Задача о многоруком бандите объясняется просто. Представим, что в зале казино игрок может выбрать тот или иной автомат (который называется рукой). К примеру, одна рука даёт некий выигрыш с вероятностью 3 процента, а другая — вдвое больший выигрыш с вероятностью 1 процент. Заранее эти вероятности и размеры вознаграждений не известны. Цель — определить наиболее выигрышную руку ^{[White-13, 14]}.

К такой задаче сводится большое множество прикладных проблем: выбор рекламных баннеров, оценка количества потребляемой животными энергии в условиях её ограничения, оценка доходности биржевых опционов, выбор наилучшего варианта лечения, изучение влияния наказаний и вознаграждений на поведение и т. д. Оптимальное решение потребовало бы больших затрат ресурсов, но можно получить субоптимальное ^{[Дэвидсон-Пайлон-19, 196]}.

В книге «Bandit Algorithms for Website Optimization» («Бандитские алгоритмы для оптимизации веб-сайтов») рассказывается история [White-13, 1—4] о некой Деборе Нал (Deborah Knull), которая владеет сайтом. Большую часть её дохода приносит этот сайт. В попытках заработать больше она хочет изменить логотип. Дебора обращается к своим знакомым и просит у них совета.

Исследователь Синтия советует провести контролируемый эксперимент — A/B-тестирование. Бизнесмен Боб выступает против «знания ради знания» и рекомендует испытать только самые надёжные из новых вариантов или не испытывать никаких, если нет уверенности: слишком велик риск потерять клиентов. Оскар, специалист по исследованию операций, советует обратить внимание на другие методы вместо традиционного A/B-теста (который вначале сильно привязывается к лучшему наблюдаемому варианту).

Исследование может дать потенциал, но требует денежных трат, а использование может вследствие неведения потенциала привести к стагнации. Нужно искать компромисс между исследованием и использованием (explore–exploit dilemma). Классический A/B-тест предполагает короткий этап исследования и долгий этап использования. В бандитских алгоритмах нет этого резкого перехода ^{[White-13, 9]}.

Общая схема

Каждый бандитский алгоритм работает по одному принципу. Многократно повторяется ряд действий:

1. Выбрать руку.
2. Получить вознаграждение.
3. Запомнить выбранную руку и полученное вознаграждение.

Все алгоритмы отличаются в основном только способом, как выбрать руку, и параметрами.

Метрики

Каждый из исследуемых далее алгоритмов имеет графики для четырёх метрик (горизонт установлен в 250 испытаний).

1. Вероятность выбора оптимальной руки.
2. Среднее вознаграждение.
3. Суммарное вознаграждение.
4. Совокупное сожаление.

Пусть \(w_{\mathrm{opt}}\) — вероятность выбора оптимальной руки. Тогда совокупное сожаление (total regret) определяется как разница между вознаграждением от выбора оптимальной руки в течение \(T\) итераций и вознаграждением от выбора в течение \(T\) итераций другой стратегии:

$$R_{T}=\sum_{i=1}^{T}\left(w_{\mathrm{opt}}-w_{i}\right)=Tw_{\mathrm{opt}}-\sum_{i=1}^{T}w_{i}$$

Также существует понятие ожидаемого совокупного сожаления, которое представляет собой матожидание совокупного сожаления:

$$R_{T}^{-}=E[R_{T}]$$

Утверждается, что ожидаемое совокупное сожаление любой не оптимальной стратегии ограничено снизу логарифмически, то есть \(E[R_{T}]=\Omega(\mathrm{log}~T)\). Поэтому стратегии с логарифмически растущим сожалением решают поставленную задачу ^{[Дэвидсон-Пайлон-19, 203]}.

Эпсилон-жадный алгоритм

Жадные алгоритмы на каждом этапе выбирают наилучший из вариантов, даже если это может привести к нежелательным последствиям в будущем. Эпсилон-жадный алгоритм является почти жадным. Параметр \(\varepsilon\) (обычно малое число, которое должно лежать в пределах между 0 и 1) означает вероятность, с которой алгоритм выполняет исследование, а не использование ^{[White-13, 11]}.

История этого алгоритма неясная, но он популярен и широко используется в обучении с подкреплением ^{[Lattimore-20, 95]}.

• С вероятностью \(1-\varepsilon\) использовать вариант, который на данный момент наилучший.
• С вероятностью \({\displaystyle \frac{\varepsilon}{N}}\) исследовать один из вариантов, то есть руку.

При \(\varepsilon=1\) получается простой A/B-тест, при \(\varepsilon=0\) — чисто жадный алгоритм ^{[Брюс-19, 136]}.

Далее представлен код на языке R.

select.arm.epsilon.greedy <- function(epsilon.greedy) {

    ifelse (runif(1, 0, 1) > epsilon.greedy$epsilon,

        which.max(epsilon.greedy$values),

        sample(1:length(epsilon.greedy$values), 1))

}

Этап обновления, как сказано выше, по большей части одинаковый для всех алгоритмов.

update.generic <- function(algorithm, arms, chosen.arm, reward, eta = 1) {

    algorithm$counts[chosen.arm] <- eta * algorithm$counts[chosen.arm] + 1

    algorithm$n <- algorithm$n + 1

    n <- algorithm$n

    value <- algorithm$values[chosen.arm] * eta

    algorithm$values[chosen.arm] <- ((n - 1) / n) * value + reward / n

    algorithm

}

Ниже показаны графики для \(\varepsilon=0{,}1\) (самый тёмный оттенок), \(0{,}2,\) \(0{,}3,\) \(0{,}4,\) \(0{,}5\) (самый светлый оттенок). График среднего вознаграждения (верхний правый) по форме схож с графиком вероятности вознаграждения (верхний левый), но имеет другой масштаб, поскольку в модели заданы следующие вознаграждения: \(1, 1, 1, 1, 2\) с вероятностями \(0{,}3,\) \(0{,}2,\) \(0{,}1,\) \(0{,}2,\) \(0{,}9\). Выполняется 5000 симуляций, берётся среднее значение.

В алгоритм можно добавить понятие темпов обучения \(\eta\), по умолчанию равный 1. Если \(\eta<1\), алгоритм быстрее «забывает» предыдущие выигрыши, если \(\eta>1\), поведение алгоритма становится более «рискованным» ^{[Дэвидсон-Пайлон-19, 205]}.

Softmax-алгоритм

Эпсилон-жадный алгоритм при случайном выборе даёт вариантам одинаковую вероятность \({\displaystyle \left(\frac{\varepsilon}{N}\right)}\), то есть не учитывает, что одна рука в какой-то момент лучше другой. Такая стратегия приведёт к избытку исследования.

Пусть \(r_{i}\) — это количество раз, которое алгоритм выбрал \(i\)-ю руку. Тогда вероятность выбора руки определяется пропорционально этому количеству ^{[White-13, 34]}, составим формулу для \(N\) рук:

$$p_{i}=\frac{r_{i}}{{\displaystyle \sum_{k=1}^{N}r_{k}}}$$

Однако для каждой величины изменяется масштаб, получается функция softmax — обобщение логистической функции.

$$p_{i}=\frac{\mathrm{exp}(r_{i})}{{\displaystyle \sum_{k=1}^{N}\mathrm{exp}(r_{k})}}$$

Следующий шаг — введение коэффициента масштабирования \(\tau\), который называется температурой.

$$p_{i}=\frac{\mathrm{exp}\left(\frac{r_{i}}{\tau}\right)}{{\displaystyle \sum_{k=1}^{N}\mathrm{exp}\left(\frac{r_{k}}{\tau}\right)}}$$

select.arm.softmax <- function(softmax) {

    z <- sum(exp(softmax$values / softmax$temperature))

    probabilities = exp(softmax$values / softmax$temperature) / z

    categorical.draw(probabilities)

}

Ниже показаны графики для \(\tau=0{,}1\) (самый тёмный оттенок), \(0{,}2,\) \(0{,}3,\) \(0{,}4,\) \(0{,}5\) (самый светлый оттенок).

Softmax-алгоритм с имитацией отжига

Отжиг (annealing) — быстрое нагревание металла и последующее медленное остывание, что делает материал крепче. Снижение температуры \(\tau\) будет означать снижение доли исследования со временем ^{[White-13, 14]}. Стратегия может быть и иной.

$$\tau = \frac{1}{\mathrm{ln}\left({\displaystyle \sum_{i=1}^{N}r_{i}+1}\right)}$$

select.arm.annealing.softmax <- function(annealing.softmax) {

    t <- sum(annealing.softmax$counts) + 1

    annealing.softmax$temperature <- 1 / log(t + 0.0000001)

    select.arm.softmax(annealing.softmax)

}

Алгоритм UCB1

Из семейства UCB (upper confidence bound — верхняя граница доверительного интервала) рассмотрим алгоритм UCB1. Он не использует случайные значения и не имеет настраиваемых параметров. Нужно учитывать, что максимальное вознаграждение — 1, в противном случае их нужно нормализовать ^{[White-13, 49]}.

UCB1 сперва исследует каждую руку. Затем для каждой руки рассчитывается метрика, которая представляет сумму среднего выигрыша руки и некой дополнительной величины.

Дополнительная величина вытекает из неравенства Хёфдинга, которое задаёт верхнюю границу вероятности того, что сумма случайных величин отклоняется от своего математического ожидания:

$$P(\mu_{i}>\hat{\mu}_{t,i}+U_{t,i})\leqslant\mathrm{exp}\left(-2tU_{t,i}^{2}\right),$$

где \(\mu_{i}\) — среднее вознаграждение \(i\)-й руки, а \(\hat{\mu}_{t,i}\) — наблюдаемое среднее вознаграждение в момент \(t\), \(U_{t,i}\) — расстояние от среднего до верхней границы доверительного интервала для \(i\)-й руки. Пусть \(p=\mathrm{exp}(-2tU_{t,i}^{2})\), тогда:

$$U_{t,i}=\sqrt{-\frac{\mathrm{log}~p}{2t}}.$$

Величина \(t\) заменяется на \(n_{i}\) — количество раз, которое рука была выбрана, а \(p\) (вероятность того, что среднее выше верхней границы доверительного интервала) — на \(t^{-4}\), небольшую вероятность (такая функция быстро сходится к нулю). Так получается величина \(c_{i}\) (назовём её «любопытство», curiosity) [LeDoux-20]:

$$c_{i}=\sqrt{\frac{2 \mathrm{ln}(s)}{r_{i}}}, s={\displaystyle \sum_{i=1}^{N}r_{i}}.$$

Она показывает, насколько меньше известно об этой руке по сравнению с другими.

select.arm.ucb1 <- function(ucb1) {

    unexplored.arms <- which(ucb1$counts == 0)

    if (length(unexplored.arms) > 0 && unexplored.arms != 0) {

        return(unexplored.arms[1])

    }

    n.arms <- length(ucb1$counts)

    ucb1.values <- rep(0, n.arms)

    total.counts <- sum(ucb1$counts)

    for (arm in 1:n.arms) {

        curiosity <- sqrt((2 * log(total.counts)) / ucb1$counts[arm])

        ucb1.values[arm] <- ucb1$values[arm] + curiosity

    }

    which.max(ucb1.values)

}

График, который показывает, как часто алгоритм выбирает лучшую руку, выглядит зашумлённым. Время от времени алгоритм «понимает», что информации о какой-то руке недостаточно, и исследует её. Это объясняет «откаты».

Алгоритм EXP3

Аббревиатура EXP3 расшифровывается как Exponential-weight algorithm for Exploration and Exploitation (экспоненциально-взвешенный алгоритм исследования и использования). Наличие весов сближает этот алгоритм с традиционными алгоритмами машинного обучения. Большие веса назначаются лучшим рукам, но изначально у каждой руки вес \(w_{i,0}=1\). Гиперпараметр \(\gamma\in(0,1]\) управляет степенью случайности исследования [LeDoux-20].

Для каждой руки рассчитывается вероятность, в соответствии с ними выбирается случайная рука:

$$p_{i,t}=(1-\gamma)\frac{w_{i,t}}{{\displaystyle \sum_{j=1}^{N}w_{j,t}}}+\frac{\gamma}{k}.$$

exp3.probabilities <- function(exp3) {

    sum.of.weights <- sum(exp3$weights)

    n.arms <- length(exp3$weights)

    probabilities <- c(length = n.arms)

    probabilities[1:n.arms] <- ((1 - exp3$gamma) * exp3$weights[1:n.arms]) /

        sum.of.weights + exp3$gamma / n.arms

    probabilities

}

После того как исход становится известен, все веса пересчитываются:

$$w_{i,t+1}=w_{i,t}\mathrm{exp}\left(\frac{\gamma\hat{x}_{i,t}}{N}\right),$$

$$\hat{x}_{i,t}= \left\{ \begin{array}{c} {\displaystyle \frac{x_{i,t}}{p_{i,t}}},i=a_{t},\\ 0, \mathrm{otherwise}.\\ \end{array} \right.$$

$$\hat{x}_{i,t}= \begin{cases*} \frac{x_{i,t}} & $i=a_{t}$,\\ 0 & otherwise \end{cases*}$$

Функция выбора руки тривиальна.

select.arm.exp3 <- function(exp3) {

    categorical.draw.mc(exp3.probabilities(exp3))

}

Но появляется сложная функция обновления весов.

update.exp3 <- function(exp3, arms, chosen.arm, reward) {

    n.arms <- length(arms)

    rewards <- c(length = n.arms)

    for (i in 1:n.arms) {

        rewards[i] <- arms[[i]]$reward

    }

    reward <- reward / max(rewards)

    probabilities <- exp3.probabilities(exp3)

    for (i in 1:n.arms) {

        estimated.x <- ifelse(i == chosen.arm, reward / probabilities[i], 0)

        exp3$weights[i] <- exp3$weights[i] *

            exp((exp3$gamma * estimated.x) / n.arms)

    }

    

    update.generic(exp3, arms, chosen.arm, reward)

}

Ниже показаны графики для \(\gamma=0{,}2\) (самый тёмный оттенок), \(0{,}4,\) \(0{,}6,\) \(0{,}8,\) \(1{,}0\) (самый светлый оттенок).

Байесовские бандиты

Байесовская статистика — очень интересная дисциплина со своим взглядом на вещи. Сперва нужно задать априорные распределения вероятностей выигрыша для разных рук ^{[Дэвидсон-Пайлон-19, 196]}.

Алгоритм сводится к циклическому повторению ряда действий.

1. Извлечь выборку \(X_{i}\) из распределения для \(i\)-й руки.
2. Выбрать руку с максимальной выборкой. \(B = \mathrm{argmax}~X_{i}\), к примеру, через матожидание \(\mu={\displaystyle \frac{\alpha}{\alpha+\beta}}\).
3. Обновить распределение.

Изначально о руках ничего не известно, поэтому априорным распределением будет служить равномерное распределение на отрезке от 0 до 1, а точнее его обобщение — бета-распределение \(\mathrm{Beta}(\alpha=1, \beta=1)\).

Если априорное распределение — это бета-распределение \(\mathrm{Beta}(\alpha, \beta)\), а данные имеют распределение Бернулли (\(X\sim\mathrm{Bernoulli}(\theta))\), то апостериорное распределение будет известно в аналитическом виде: \(\mathrm{Beta}\left(\alpha+{\displaystyle \sum_{i=1}^{n}x_{i}}, \beta+n-{\displaystyle \sum_{i=1}^{n}x_{i}}\right)\). При \(n=1\) получается распределение \(\mathrm{Beta}(\alpha+x, \beta+1-x)\) ^{[Дэвидсон-Пайлон-19, 152]}.

Откуда следует вывод, что если априорное распределение \(\mathrm{Beta}(\alpha=1, \beta=1)\), то апостериорное распределение после первой итерации — \(\mathrm{Beta}(\alpha=1+x, \beta=1+1-x)\).

select.arm.bayesian <- function(bayesian) {

    which.max(bayesian$alpha / (bayesian$alpha + bayesian$beta))

}

update.bayesian <- function(bayesian, arms, chosen.arm, reward) {

    bayesian$alpha[chosen.arm] <- bayesian$alpha[chosen.arm] + reward

    bayesian$beta[chosen.arm] <- bayesian$beta[chosen.arm] + 1 - reward

    update.generic(bayesian, arms, chosen.arm, reward)

}

На анимированной иллюстрации показано, как изменяются пять распределений (соответствующих рукам).

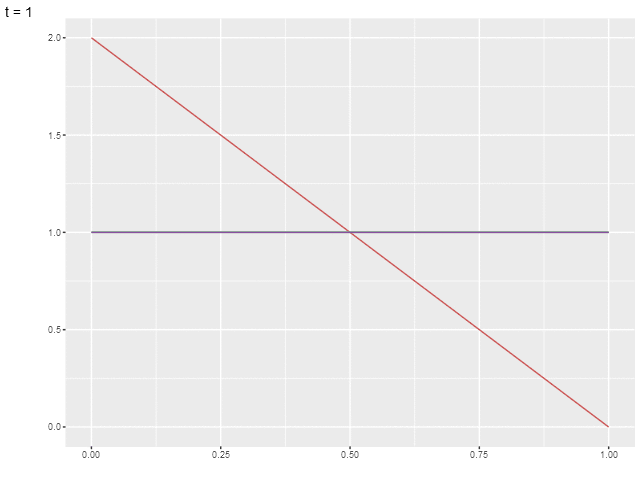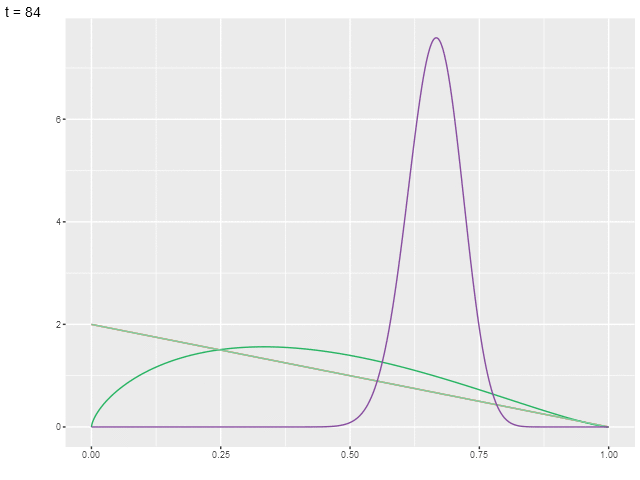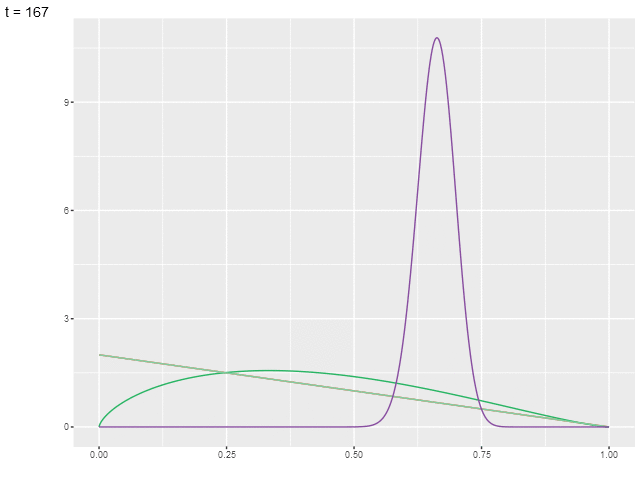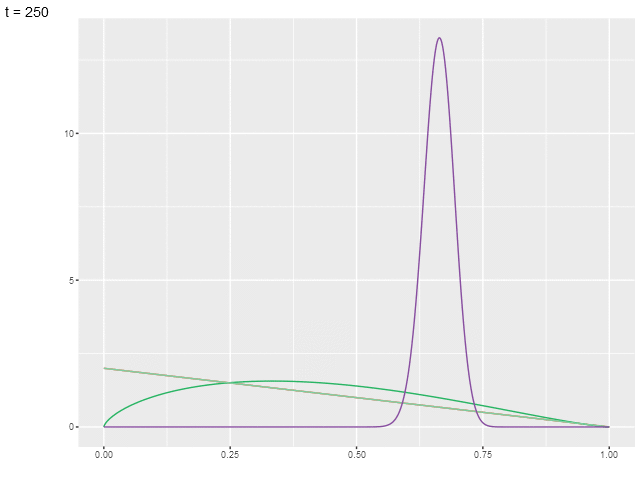
Байесовский алгоритм UCB

Предположим, что вознаграждения распределены нормально (при возрастании гиперпараметров бета-распределения оно схоже с нормальным). Тогда разница между средним и верхней границей доверительного интервала будет равна [LeDoux-20]:

$$c_{i}=\frac{c\sigma(r_{i})}{\sqrt{n_{i}}},$$

где \(\sigma(r_{i})\) — среднеквадратическое отклонение вознаграждения \(i\)-й руки, а \(c\) — настраиваемый гиперпараметр, для доверительного интервала шириной 95 процентов \(c=1{,}96\).

select.arm.bayesian.ucb <- function(bayesian.ucb) {

    unexplored.arms <- which(bayesian.ucb$counts == 0)

    if (length(unexplored.arms) > 0 && unexplored.arms != 0) {

        return(unexplored.arms[1])

    }

    n.arms <- length(bayesian.ucb$counts)

    bayesian.ucb.values <- rep(0, n.arms)

    total.counts <- sum(bayesian.ucb$counts)

    for (arm in 1:n.arms) {

        stderr <- sqrt(bayesian.ucb$dispersion[arm])

        curiosity <- bayesian.ucb$scale * stderr /

            sqrt(bayesian.ucb$counts[arm])

        bayesian.ucb.values[arm] <- bayesian.ucb$values[arm] + curiosity

    }

    which.max(bayesian.ucb.values)

}

update.bayesian.ucb <- function(bayesian.ucb, arms, chosen.arm, reward) {

    bayesian.ucb <- update.generic(bayesian.ucb, arms, chosen.arm, reward)

    

    dispersion <- bayesian.ucb$dispersion[chosen.arm]

    n <- bayesian.ucb$n - 1

    bayesian.ucb$dispersion[chosen.arm] <- ((n - 1) / n) * dispersion +

        (reward - bayesian.ucb$count[chosen.arm]) ^ 2 / n

    bayesian.ucb

}

Сравнение алгоритмов

Графики совокупного сожаления (чем меньше, тем лучше). Параметры: для эпсилон-жадного алгоритма \(\varepsilon=0{,}2\), для Softmax-алгоритма \(\tau=0{,}2\), для алгоритма Exp3 \(\gamma=1\).

Модификации

Можно задействовать байесовских бандитов как надстройку к другим алгоритмам, то есть получаются иерархические алгоритмы. Сверху находится некий алгоритм для выбора байесовских бандитов нижнего уровня (различающихся, к примеру, параметром \(\eta\)). Такие модели неявно выбирают руку для испытания. А на основе того, выиграл ли байесовский бандит нижнего уровня, происходит корректировка бандитов верхнего уровня ^{[Дэвидсон-Пайлон-19, 205]}.

Приложение: исходный код.

Литература

[b][White-13][/b] John Myles White. Bandit Algorithms for Website Optimization. O’Reilly. 2013. 87 pages. Интересный факт: на обложке изображён бандикут.

[b][Lattimore-20][/b] Tor Lattimore, Csaba Szepesvári. Bandit Algorithms. Cambridge University Press. 2020. 594 pages.

[b][Брюс-19][/b] Брюс П. Практическая статистика для специалистов Data Science: Пер. с англ. / П. Брюс, Э. Брюс. — СПб.: БХВ-Петербург, 2019. — 304 с.: ил.

[b][Дэвидсон-Пайлон-19][/b] Дэвидсон-Пайлон К. Вероятностное программирование на Python: байесовский вывод и алгоритмы. — СПб.: Питер, 2019. — 256 с.: ил. — (Серия «Библиотека программиста»).

[b][Грас-20][/b] Грас Дж. Data Science. Наука о данных с нуля: Пер. с англ. — СПб.: БХВ-Петербург, 2020. — 336 с.: ил.

[b][LeDoux-20][/b] James LeDoux. Multi-Armed Bandits in Python: Epsilon Greedy, UCB1, Bayesian UCB, and EXP3. https://jamesrledoux.com/algorithms/bandit-algorithms-epsilon-ucb-exp-python/.

Ссылки

Интерактивные примеры эпсилон-жадного и UCB1-алгоритма с графиками среднего вознаграждения: https://pavlov.tech/2019/03/02/animated-multi-armed-bandit-policies/.

Визуализация эпсилон-жадного алгоритма и UCB1: https://cse442-17f.github.io/LinUCB/.

Блог banditalgs.com.

Пример использования библиотеки для эпсилон-жадного алгоритма с графиком совокупного сожаления: https://nth-iteration-labs.github.io/contextual/articles/epsilongreedy.html.